Bob Somerby wants to know if the logician/mathematician Kurt Gödel is a genius or a charlatan. The answer is "genius," but it's hard for non-mathematicians to understand his seminal theorem or why it matters. Bob is relying on Rebecca Goldstein's biography of Gödel, and this is a mistake since it's a biography, not a mathematical treatise.
But it's dex night, so I'll take a crack at it. Fair warning: you really need to have at least a little bit of background in math to understand this. There's just no way around it. However, you don't need much as long as you're willing to tolerate a bit of mathematical symbology. Here goes.
1. Mathematical symbols
Although most of us don't think of it this way, mathematics is actually a formal logical system of symbol manipulation.¹ For this to work, it must be possible to express all mathematical statements in a formal symbolic language. And it is! Take this statement, for example:
For every number there is a number that's one higher
In mathematical symbology it looks like this:
∀ x ∃ x + 1
(For all numbers x there exists x + 1)
There is a symbol for anything you can say in the language of mathematics. If you're interested, a complete list is here—though there are some complicated nuances for certain kinds of expressions. Basically, though, there's a symbol for everything, although non-mathematicians are unfamiliar with most of them.
2. Gödel numbering
Gödel's initial insight was that you could assign a unique number to every symbol. Here's a sample:
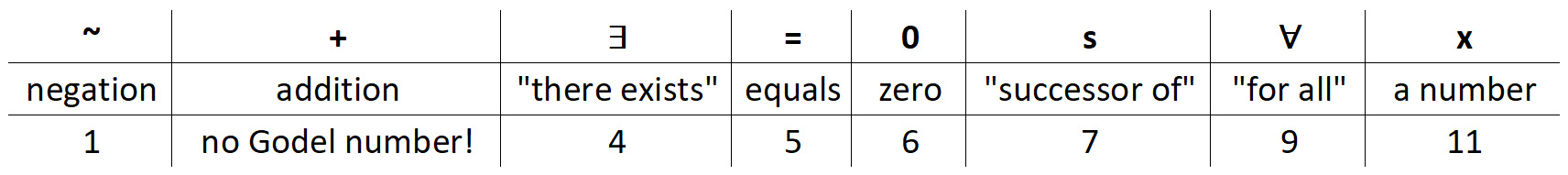After a bit of rewriting to mathematical standards, our statement from above looks like this:
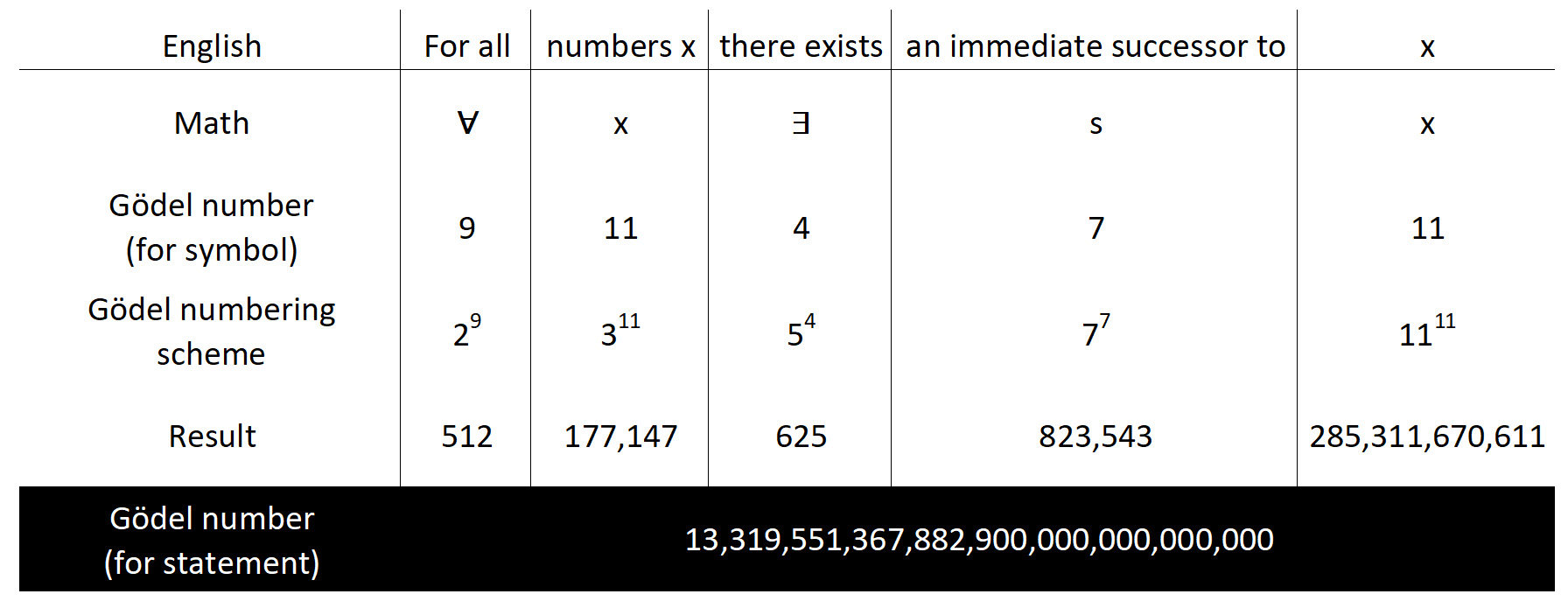In essence, Gödel numbering is simple. In line 3 we replace every symbol with its Gödel number. In line 4, we take a series of prime numbers starting with two, and raise each one to its Gödel number. The first prime is 2, so we calculate 29. The next prime is 3, so we calculate 311. Etc.
In the final line we multiply all these numbers together to get the Gödel number for the entire statement. It's a big number, and for more complicated statements the number becomes astronomical. But who cares? We don't actually have to calculate this number, we just have to know that it exists and that it's unique. Which it is. That final number represents our statement, only our statement, and there's no other number that also represents our statement. This number is our statement.
3. Gödel's proof
So far, what Gödel has done is inventive and easy to understand. What comes next is world historically insightful and more or less impossible to understand for non-mathematical laymen. But let's go ahead with a simplified version.
Every mathematical system—arithmetic, geometry, set theory, etc.—consists of (1) a set of symbols, (2) a set of rules for constructing statements that are valid expressions (i.e., strings of symbols) but which may be either true or false, (3) a set of rules for manipulating symbols, and finally, (4) a set of axioms to start with. This is called an "axiomatic system," and it's the foundation of nearly all modern mathematics.
A formal proof of a theorem starts with axioms (in symbolic form) and then moves in small steps using valid statements that are created using the rules of manipulation. When this series of statements finally reaches the theorem itself, the theorem is said to be proven.
Any respectable system of mathematics must fulfill two requirements: it must be complete and it must be internally consistent. "Complete" means that every true theorem can be proven. "Consistent" means that it's not possible to prove both a theorem and its opposite. But how do you prove that a mathematical system is both complete and consistent?
It's not easy! David Hilbert, the namesake of one of my cats, famously created an axiomatic system of geometry in 1899, and in 1910 the philosopher/logician Bertrand Russell and his coauthor Alfred North Whitehead produced a massive three-volume work called Principia Mathematica, which attempted to completely systematize arithmetic and set theory and make them both complete and free of contradictions. Along the way, Russell and Whitehead created a remarkably comprehensive system of notation that allowed all statements of arithmetic to be written in a standard manner. It is one of the most famous treatises on logic and mathematics ever written.
But was it correct? In the same way that individual symbols and statements can be reduced to Gödel numbers, an entire proof can also be given a unique Gödel number. Gödel's genius was in realizing that certain properties of these numbers could tell us things. In particular, they could be used to decide whether a system of mathematics was complete and consistent.
And it turns out that no interesting system of mathematics is both. In 1931 Gödel published a famous paper which showed, using Gödel numbers, that assertions about mathematics (for example, "the series of statements with Gödel number x is a proof of the formula with Gödel number y") could be reduced to ordinary statements within mathematics ("x is related to y"—though in a complicated way that we will skip over lightly). This in turn allowed Gödel to demonstrate that in any system of mathematics complex enough to be useful—such as ordinary arithmetic—you can construct at least one statement about arithmetic that (1) can be transformed into a normal statement within arithmetic, (2) can be proven, but (3) only if its opposite can also be proven. That's impossible in any consistent system, which means the statement is unprovable in an allegedly consistent system like arithmetic. But Gödel did more: he showed that even though this statement couldn't be proven, it was clearly true. This means that arithmetic is incomplete: it contains true statements that can't be proven.
Finally, in his coup de grâce, Gödel showed that the statement "arithmetic is consistent" is unprovable within the system of arithmetic itself. In all this he used the notation created in Principia Mathematica, which had been explicitly designed to create a system of arithmetic and formal logic that was complete and internally consistent. The result was a proof that Russell and Whitehead were wrong. No system of mathematics is both complete and consistent.
That was a kick in the gut.
4. But what does it all mean?
In day-to-day use, Gödel's theorem plays no role. In fact, a few years after it was published a fellow German mathematician proved that for all practical purposes the system of arithmetic we use (based on the Peano postulates, a set of five axioms for the natural numbers created by Giuseppe Peano in 1889) is indeed consistent. Workaday math is in fine shape, and most working mathematicians go through life never knowing anything about Gödel, who is of interest mostly to abstract logicians.
But on an abstract level Gödel's theorem was both a bombshell and a source of dismay. What's more, it does come into play sometimes in fairly ordinary mathematics.² For example, transfinite math defines various types of infinity, and the two smallest types of infinity correspond to the set of integers (represented as ℵ0, or "aleph nought," because mathematicians like to fuck with us) and to the set of real numbers (represented as C, because mathematicians like to fuck with us). But is there any infinity between those two? In 1966 Paul Cohen won a Field Medal for using Gödel's theorem to show that this was impossible to prove one way or another.
(This is called the Continuum Hypothesis, first proposed by Georg Cantor, the inventor of transfinite mathematics. He believed there was no infinity between ℵ0 and C, and this was #1 on David Hilbert's famous list of 23 unsolved problems that he presented to the mathematical community in 1900. As of today, eight of these problems have been fully proven; three are still unproven; ten are partially proven; and two have been tossed out for being too vague.)
Long story short, Gödel's theorem is both enormously important but also of little use in real life. This is the way of things.
5. Further Reading
If you really want to understand what Gödel did, the indispensable book is Gödel's Proof, by Ernest Nagel and James Newman. It was published the year I was born and is still in print. It does require a modest love of math, but it's only a hundred pages long and is written unusually clearly. Another possible text is Douglas Hofstadter's Gödel, Escher, Bach, which is massively long but also very entertaining. It's not everyone's cup of tea, but it does demonstrate how Gödel's theorem works, and it gets there in very tiny, non-mathematical steps.
¹Actually there isn't one formal system of mathematics, there are many. There's one for geometry, one for set theory, one for arithmetic, etc.
²I am, obviously, using "fairly ordinary" in a very specific sense.
Check out Natalie Wolchover's article How Gödel’s Proof Works over on Quanta magazine, a periodical about which I have very mixed feelings.
Damn, when I was 17 I did real well on a mathematics competition. 64 years later I'm afraid I'll have to take your word for it. Aging is terrible.
This post reminds me of studying “Grundy numbers” in college.
And here today I have no clue what a “Grundy number” even is. But I do remember studying them.
It's way overused like Schrodinger's cat.
It's way overused like Schrodinger's cat and people make too much of a big deal out of it.
"For every number there is a number that's one higher"
Don't use "number" here!
"There's one for geometry." Au contraire, mon frere! There are several!
I use a completely non-mathematical approach when explaining this to non-mathematical friends.
Consider the following sentence: "This statement is false."
It's easy for anyone to see that the statement is neither true nor false. Gödel used a variation of this sentence as the basis of his 1st Incompleteness Theorem: "This statement cannot be proven." He went on to show, using mathematics itself, that any useful system of mathematics must contain these kinds of statements.
I then tell them that going beyond this level requires math, and that's usually enough to satisfy them.
Pretty much the way I would describe it as well. Self reference is a critical point here. And it wasn't at all obvious that it was possible.
This is how I learned it as well. Godel basically showed that the statement "This statement has no proof" existed. If true, it is a true statement that has no proof. If false, it is a false statement that has a proof, which means that the proof system is inconsistent (you're not supposed to be able to prove false statements in any proof system).
That sounds right to me.
The magic of Gödel numbering is that it lets you take statements in the metalanguage ("such and such a thing is a proof", for example) and convert them to the formulas in the language (an arithmetical statement). Fixed point theorems then let you encode self-referential statements. And hey presto, you're done!
"This statement is false" - is self-referential and there is debate about whether or not such statements should be allowed. There are mathematical systems that exclude self-referential elements. Bertrand Russel tried to avoid self-referential logic by introducing a series of "types" so that a higher tier (think meta) could describe lower types. It was something of a kludge.
If you accept self-referencialism, then Godel is your guy. I do not accept it even though it means abandoning large swaths of mathematics (e.g. least upper bound). But I'm a fan of Kronecker and Brouwer.
Another book I would recommend: "What is the name of this book", by Raymond Smullyan.
Smullyan is (was?) a world class logician and magician, and a great inventor of riddles. It is a book full of amusing stories and logic puzzles, which start simple and get more complicated as you go along. One of the last chapters guides you to an explanation of Godel's theorem, again through puzzles. A real tour de force, and highly entertaining.
It is well-known that that there is a mistake in the Nagel & Newman book that leads to a serious misrepresentation of the the (first) Godel theorem. (I mean no disrespect to Nagel, who was one of my undergraduate teachers.)
There are some clever books by one of the Smullyans (Raymond, I think) that have a number of elegant simplified versions of the original proof.
Steve_OH above adds a crucial bit to your account by connecting the proof to the liar paradox. That's really the key, as I understand it, along with the idea of a formal system of derivation.
Just for the hell of it, let me mention that in the late 1940s Godel discovered solutions to the field equations of general relativity which permit closed timelike curves. That is, one can start a point p in spacetime, travel alwlays to the future, and eventually arrive at point p (again?). I think it's fair to say that there is not as yet any satisfactory understanding of this. His friend A. Einstein dismissed this solution as "unphysical", but it's not clear what that means.
That's just the well-known result that if the universe has non-zero angular momentum (read: if it's rotating about some axis), then it is possible to travel backwards in time by traversing some path a a speed less than the speed of light. See also the Ehrenfest Disk.
Godel's work is highly significant to those of us in computing.
I think that Godel's incompleteness theorem is the progenitor of Turings proof of the undecidability of the Halting Problem.
This IS consequential. It generalizes fairly easily, and calls out a huge class of functions that we would in fact, love to be able to write programs to implement, but we can't.
Can Not Write.
I mean, yeah, it doesn't help you do a calculation - it tells you not to waste your time trying to do that.
And furthermore Godel was the first to demonstrate encoding formulas as numbers, and that that could lead to self reference. Programs self-reference a lot these days, and would do it more if it wasn't so chaotic and unpredictable.
Absolutely.
Ugh, and I thought a year of college calculus was hard. Actually, I think Kevin's done a pretty good job of bringing along the slightly mathematically challenged to an general understanding of Godel numbers, and why they mean anything to anyone.
High school students think that calculus represents the peak of mathematical mind-bending complexity. But no, it's just the peak of what you can hope to grasp as a high school student. It's insignificant compared to the truly mind-bending stuff.
It's not even calculus; it's a grab bag of techniqus. Real analysis (you see what I did there) doesn't typically start until your junior or senior year as an undergraduate.
Here I thought the representations were the result of mathematicians being lazy writers with horrible penmanship. And that they had very little grasp of fucking with anything beyond arm's reach 🙂
They need to add Rube Goldberg to the group.
Why here, why now? WTF, is this just simple self-validation, a bit of carnival barking, or an afternoon off from politics and what used to be called graphs? Maybe Godel is an insistent worm inside the blogmeister that he simply must deal with or go mad?
I think this post is just a man coming off the high of briefly thinking of himself as someone with an apartment in Paris. I am a man with an apartment in Paris, so let me kick out the jams. True enough, I am born and basted in suburban Los Angeles, and I live in a tract next to an artificial lake watered with the the water of a thousand almond trees, but I am a man with an apartment in Paris, there isn't much difference between me and Aristide Briand, and I am now gonna explain Godel to you honyockers, whether you like it or not..
The motivation is pretty clear, and it's good motivation. I got nothing against the motivation, Paris is neat. But please spare me the Godel.
Nice summary! I've been reading Godel, Escher, Bach for years now. Still not finished but as you said, it's very entertaining.
" because mathematicians like to fuck with us"
Because we've worked our way through the Latin and Greek alphabets so now, in search of unique symbols, we're working on Hebrew.
BTW, I once knew an old dude who knew Einstein and Godel when they were in Princeton. He claimed to have discovered them, totally gaslit, down on their knees playing marbles.
i think your definition of gaslit is different from mine.
veritasium had a good godel video https://www.youtube.com/watch?v=HeQX2HjkcNo
Outstanding. And also touches on Cantor, Hilbert and Turing.
OT: This is your last chance to convince Biden that a gas tax holiday is the wrong-headed policy to pursue, as it undercuts all attempts to decarbonize our economy while doubling down on supporting an unsupportable demand-supply distortion.
OT2: Senate voted 64-34 to force cloture on the "Bipartisan Safer Communities Act" bill. I guess you were wrong?
Like it matters. Gas prices are artificially created.
He might not have been a charlatan, but just about everyone who has used his work to "prove" all sorts of shit have been charlatans.
There's another big result of Godel's theorem involving what they call modeling theory. Mathematics might just be about series of symbols, but it is also about underlying reality. Those symbols describe things. Since there are theorems that cannot be proven or disproven in every useful mathematical system, that implies that those systems of symbols must describe more than one underlying reality: at least one in which the theorem is true and at least one in which the theorem is false.
That's how the continuum hypothesis has been resolved. You can do perfectly good mathematics assuming it is true, and for the objects described by that work, the hypothesis is true. You can also do perfectly good work assuming it is false, and for the objects described by that work, that hypothesis is false.
This is a common way of resolving things in mathematics. You can build an interesting enough geometry using Euclid's first four postulates. You can assume his fifth postulate is true and produce valid mathematical statements about plane geometry. Alternately, you can assume that there are no parallel lines and wind up with something like geometry on the surface of a sphere. If you allow any number of parallel lines, you have get mathematical statements about objects with hyperbolic geometry.
This flows from modeling theory, which was developed as a corollary to Godel's result. Thinking of these alternate geometries as first class mathematical systems followed from Godel's proof. Incompleteness gives one a place to do all sorts of interesting mathematics. The ancient Greeks knew about spherical geometry, but the assumption was that it was a second class geometry only meaningful in terms of first class plane or solid geometry. Godel let mathematicians drop that class distinction.
Go on about Godel all you want, just avoid going on Godel's diet. He was mentally ill and, afraid of being poisoned, starved himself to death.
"Mathematics might just be about series of symbols, but it is also about underlying reality."
This is not a mathematical statement. It's a useful belief that's so far been very productive. But how could you possibly prove (in a mathematical sense, or even in a weaker "philosophical" sense) that "reality is mathematical"?
The best you can say is we have applied a series of increasingly sophisticated mathematical model to reality, and they've all worked well, each one better than the previous one.
Pingback: Gödel’s theoren explained | Later On
Here I was all psyched to talk about the mid-season cliffhanger on Stranger Things . . .
"In 1966 Paul Cohen won a Field Medal for using Gödel's theorem to show that this was impossible to prove one way or another."
IIRC Gödel was the one who proved that we couldn't prove that such an infinity existed (the constructible universe is a model of ZFC + CH, so it could not be that ZFC proves "not CH"). Cohen innovation was the successful proof that we can't prove that such an infinite set doesn't exist either.
You say Gödel's theorem plays no role but without it Norman the robot would have taken over the Federation https://www.youtube.com/watch?v=YbHtzqCge_8
What it ultimately proves is that math is not real in that it is not provable. It is merely a language. What the Godel/Bach/Escher book shows is that somethings devolve into themselves and so lose their external meaning. They are there but not there. Like language, math is a representation of reality. It is, therefore, quite possible to create a different math and it works.
There is a tribe, I believe in the Pacific who, if you ask them to divide a stick into three pieces they will divide it unequally. In out math, we would divide equally. For the tribe, there version allows them to function. It is as real as our math. Just like nether the English word water or the Spanish word agua is the thing itself- h2o, math is not the thing itself and is therefore merely a representation.
You don't need the proof, the point is easy to state, especially in Turing form.
Suppose I give you a mathematical statement. Is it true or is it false?
This seems like an easy question (in principle), but it's a meaningless question because there is a third option: the attempt to prove it may not be finite.
In other words I can attempt to prove the statement and I can make a sequence of deductions one after the other, all correct, but there simply is no FINITE sequence of deductions that ENDS with either true or false.
This is easier to see if we make two slight changes.
First we ask: if I give you a computer program, can you tell if it finishes or not? Obviously some simple programs can just have an endless loop, and even though a simple "let's run the program in my head" will keep going for ever, a smarter analysis can see the structure of such a loop and know that it will never end.
But we can make programs that are simple but impossible to analyze in this (or any other) way, for example:
int f(int n){
repeat{
if(n is even) n=n/2 else n=(3n+1)/2
} until n=1
}
Will this function ever end (the Collatz Conjecture)? That statement is equivalent to a mathematical theorem (unproved, perhaps unprovable).
In both versions, the point is that we do not, naively, appreciate the point that a proof is a FINITE sequence of deductions, and so a result may fail to be provable, not because it is false, but because no finite sequence of deductions proves it to be true. ie "thruthness" is three-valued
- provable true
- provable false
- unprovable because no finite sequence of deductions results in a proof.
The computer version feels more intuitive because it kinda captures experience. You may start a calculation and either it gives you the answer you hoped for, or it give you a different answer, or it just keeps going and going and after a minute, an hour, a day, you lose patience and restart.
The above explains WHAT the theorem is doing. Of course mathematically the trick is all not just in pointing out that the above (a sequence of deductions may be indefinitely long and may never end) but in showing that in fact this can happen, that there isn't some other clever magic that steps in to somehow save us, and ensures that the required sequence of steps is never longer than some finite number. That's what Godel (and in the computer form, Turing) proved.
BTW this insight (that a failure mode is possible because things grow indefinitely) is useful beyond just mathematics.
In particular many phase transitions are best understood in this way – what happens as you approach the phase transition is that certain correlated structure [domains with a different type of order from the primary phase] grow larger and larger, so that the phase transition is the point at which there average size becomes infinite and they replace (or more precisely exactly co-exist with) the primary phase, with the slightest change in conditions converting the state "indefinitely large primary state in coexistence with indefinitely large secondary state" into one of "large (but now finite) bubbles of what was primary state co-existing in indefinitely large extents of what was secondary state".
The same is even true in the social sciences where you can see certain types of co-ordination failures, for example (and so many economic effects) as phase transitions, ultimately rooted in things like co-ordination chains that grow indefinitely long. We can't say that a chain will break at a particular length, but we can say that if the links are not all finite, but the chain is grown indefinitely long, then a break will occur.
"we can say that if the links are not all PERFECT" Damn lack of editor!
FYI Godel's paper is short and straightforward. If you have a mathematical background, it's the best way to understand what he was up to.
Pingback: Weekend link dump for June 26 – Off the Kuff