Kevin Drum

This is a Louisiana egret resting in a bed of daisies that match his beak. Apparently this egret has an excellent color sense.

Over at Vox, Rachel Cohen asks:

Should you keep abortion pills at home, just in case?

With Roe on the brink, more experts are talking about advance provision of mifepristone and misoprostol.

Medication abortion, or taking a combination of the drugs mifepristone and misoprostol, is an increasingly common method for ending pregnancies in the United States....With more in-person clinics shuttering and a Supreme Court that’s threatening to overturn Roe v. Wade, a small but growing number of reproductive experts have been encouraging discussion of an idea called “advance provision” — or, more colloquially, stocking up on abortion pills in case one needs them later.

Cohen spends 1,500 words to fully answer the question in her headline, but I'll use just one: Yes. They're safe, they have a long shelf life, we have years of experience with them, and bad side effects are minimal. And the cost is low: $30-60 or so depending on where you buy them and what your insurance pays for.

As with any drug, there are precautions. WebMD has a good writeup here. Or talk to your doctor.

Generally speaking, though, I can't see any reason not to have abortion pills handy if you have any risk of having an unwanted pregnancy. If you live in California and there's a good clinic around when it happens, fine. You wasted a few bucks on some pills. If you live in Texas, it might be your only choice. So just do it. What's the argument against it?

In a review of Talent, Edward Nevraumont says:

Everywhere I have worked, the organization’s hiring processes were tilted in favor of experience over intelligence. Interviews include behavioral questions or assessments of specific skills. Rarely is anyone on the hiring loop running problem-solving sessions that require the candidate to demonstrate how they might deal with the real-world challenges they will encounter in the workplace.

That's been my experience too. And for a great many jobs it's fine. The problem is that it often goes way too far.

In sales, specifically, hiring managers not only want someone with a good track record, but a good track record within their highly specific niche of the market. This is a mistake. Just pick the best sales person! A lot of people are surprised by how quickly a new hire with smarts can get up to speed with an unfamiliar product and an unfamiliar set of clients (resellers, distributors, large customers, etc.).

I recall one especially frustrating experience trying to hire a VP of marketing to replace me. One candidate struck me as exceptionally smart, qualified, and with excellent savvy. But she didn't work in our industry. She worked in the software industry, but not our little piece of it.

I didn't think that mattered. She obviously knew the basics of selling business software, and our particular type was hardly so esoteric that it would take years to learn. Anyone talented could pick up the basics in a few months and be 90% up to speed within half a year. In the meantime, the entire rest of the company would be around to keep things on track.

But I lost that battle. My peers just couldn't stomach the thought of hiring someone whose experience was so far afield. I'm still pretty sure it was a mistake. Relevant experience is obviously important, but don't insist on it being hyper-relevant.

POSTSCRIPT: Then again, maybe they didn't like her for some reason they didn't want to admit. Maybe they didn't like the idea of a woman VP. Maybe they didn't like the color of dress she wore. Who knows?

Or maybe she wasn't as smart and qualified as I thought. Perhaps they saved me from making a bad mistake.

Bob Somerby wants to know if the logician/mathematician Kurt Gödel is a genius or a charlatan. The answer is "genius," but it's hard for non-mathematicians to understand his seminal theorem or why it matters. Bob is relying on Rebecca Goldstein's biography of Gödel, and this is a mistake since it's a biography, not a mathematical treatise.

But it's dex night, so I'll take a crack at it. Fair warning: you really need to have at least a little bit of background in math to understand this. There's just no way around it. However, you don't need much as long as you're willing to tolerate a bit of mathematical symbology. Here goes.

1. Mathematical symbols

Although most of us don't think of it this way, mathematics is actually a formal logical system of symbol manipulation.¹ For this to work, it must be possible to express all mathematical statements in a formal symbolic language. And it is! Take this statement, for example:

For every number there is a number that's one higher

In mathematical symbology it looks like this:

∀ x ∃ x + 1

(For all numbers x there exists x + 1)

There is a symbol for anything you can say in the language of mathematics. If you're interested, a complete list is here—though there are some complicated nuances for certain kinds of expressions. Basically, though, there's a symbol for everything, although non-mathematicians are unfamiliar with most of them.

2. Gödel numbering

Gödel's initial insight was that you could assign a unique number to every symbol. Here's a sample:

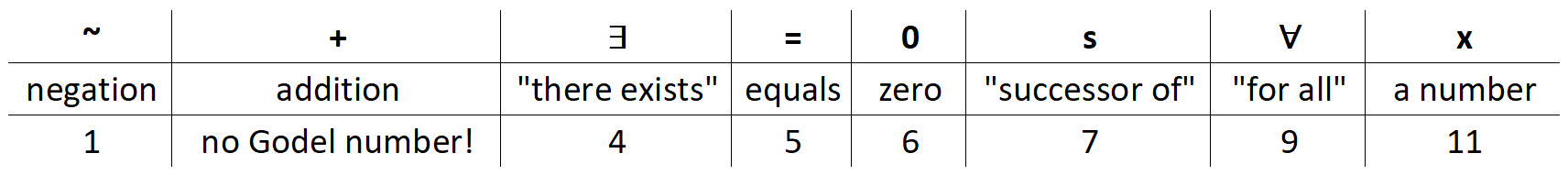After a bit of rewriting to mathematical standards, our statement from above looks like this:

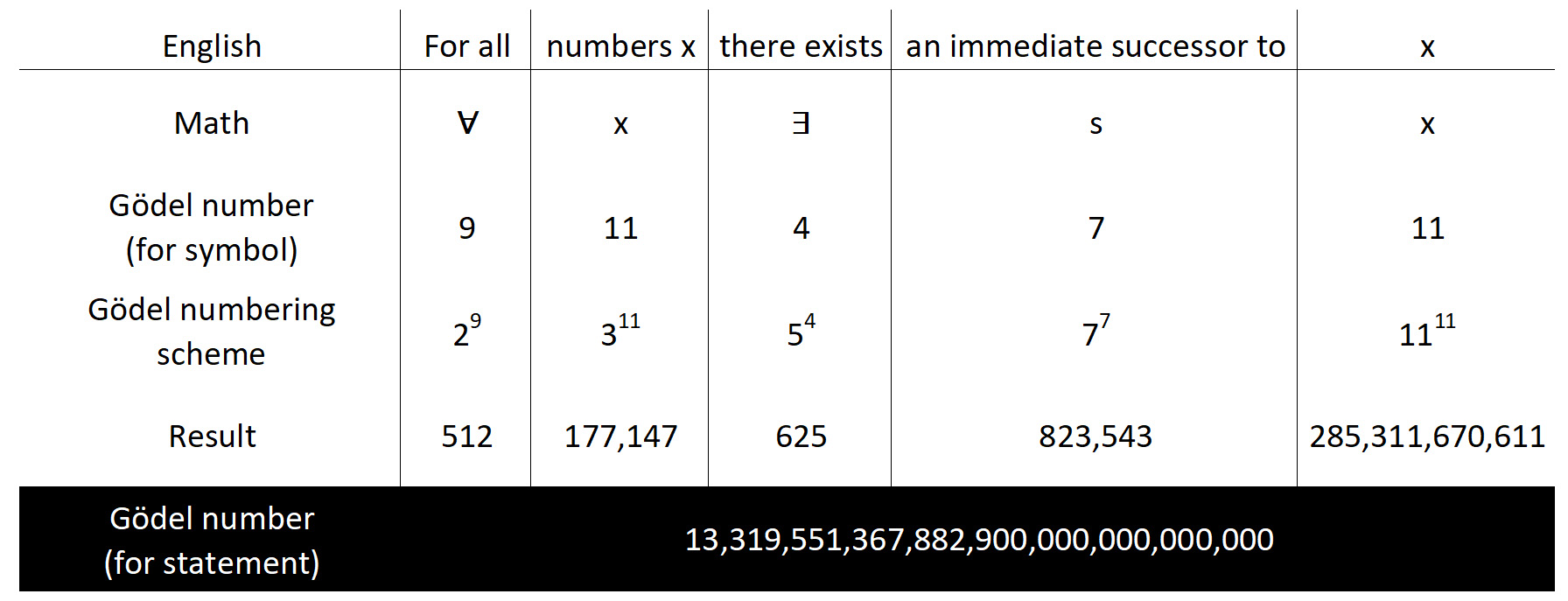In essence, Gödel numbering is simple. In line 3 we replace every symbol with its Gödel number. In line 4, we take a series of prime numbers starting with two, and raise each one to its Gödel number. The first prime is 2, so we calculate 2⁹. The next prime is 3, so we calculate 3¹¹. Etc.

In the final line we multiply all these numbers together to get the Gödel number for the entire statement. It's a big number, and for more complicated statements the number becomes astronomical. But who cares? We don't actually have to calculate this number, we just have to know that it exists and that it's unique. Which it is. That final number represents our statement, only our statement, and there's no other number that also represents our statement. This number is our statement.

3. Gödel's proof

So far, what Gödel has done is inventive and easy to understand. What comes next is world historically insightful and more or less impossible to understand for non-mathematical laymen. But let's go ahead with a simplified version.

Every mathematical system—arithmetic, geometry, set theory, etc.—consists of (1) a set of symbols, (2) a set of rules for constructing statements that are valid expressions (i.e., strings of symbols) but which may be either true or false, (3) a set of rules for manipulating symbols, and finally, (4) a set of axioms to start with. This is called an "axiomatic system," and it's the foundation of nearly all modern mathematics.

A formal proof of a theorem starts with axioms (in symbolic form) and then moves in small steps using valid statements that are created using the rules of manipulation. When this series of statements finally reaches the theorem itself, the theorem is said to be proven.

Any respectable system of mathematics must fulfill two requirements: it must be complete and it must be internally consistent. "Complete" means that every true theorem can be proven. "Consistent" means that it's not possible to prove both a theorem and its opposite. But how do you prove that a mathematical system is both complete and consistent?

It's not easy! David Hilbert, the namesake of one of my cats, famously created an axiomatic system of geometry in 1899, and in 1910 the philosopher/logician Bertrand Russell and his coauthor Alfred North Whitehead produced a massive three-volume work called Principia Mathematica, which attempted to completely systematize arithmetic and set theory and make them both complete and free of contradictions. Along the way, Russell and Whitehead created a remarkably comprehensive system of notation that allowed all statements of arithmetic to be written in a standard manner. It is one of the most famous treatises on logic and mathematics ever written.

But was it correct? In the same way that individual symbols and statements can be reduced to Gödel numbers, an entire proof can also be given a unique Gödel number. Gödel's genius was in realizing that certain properties of these numbers could tell us things. In particular, they could be used to decide whether a system of mathematics was complete and consistent.

And it turns out that no interesting system of mathematics is both. In 1931 Gödel published a famous paper which showed, using Gödel numbers, that assertions about mathematics (for example, "the series of statements with Gödel number x is a proof of the formula with Gödel number y") could be reduced to ordinary statements within mathematics ("x is related to y"—though in a complicated way that we will skip over lightly). This in turn allowed Gödel to demonstrate that in any system of mathematics complex enough to be useful—such as ordinary arithmetic—you can construct at least one statement about arithmetic that (1) can be transformed into a normal statement within arithmetic, (2) can be proven, but (3) only if its opposite can also be proven. That's impossible in any consistent system, which means the statement is unprovable in an allegedly consistent system like arithmetic. But Gödel did more: he showed that even though this statement couldn't be proven, it was clearly true. This means that arithmetic is incomplete: it contains true statements that can't be proven.

Finally, in his coup de grâce, Gödel showed that the statement "arithmetic is consistent" is unprovable within the system of arithmetic itself. In all this he used the notation created in Principia Mathematica, which had been explicitly designed to create a system of arithmetic and formal logic that was complete and internally consistent. The result was a proof that Russell and Whitehead were wrong. No system of mathematics is both complete and consistent.

That was a kick in the gut.

4. But what does it all mean?

In day-to-day use, Gödel's theorem plays no role. In fact, a few years after it was published a fellow German mathematician proved that for all practical purposes the system of arithmetic we use (based on the Peano postulates, a set of five axioms for the natural numbers created by Giuseppe Peano in 1889) is indeed consistent. Workaday math is in fine shape, and most working mathematicians go through life never knowing anything about Gödel, who is of interest mostly to abstract logicians.

But on an abstract level Gödel's theorem was both a bombshell and a source of dismay. What's more, it does come into play sometimes in fairly ordinary mathematics.² For example, transfinite math defines various types of infinity, and the two smallest types of infinity correspond to the set of integers (represented as ℵ₀, or "aleph nought," because mathematicians like to fuck with us) and to the set of real numbers (represented as C, because mathematicians like to fuck with us). But is there any infinity between those two? In 1966 Paul Cohen won a Field Medal for using Gödel's theorem to show that this was impossible to prove one way or another.

(This is called the Continuum Hypothesis, first proposed by Georg Cantor, the inventor of transfinite mathematics. He believed there was no infinity between ℵ₀ and C, and this was #1 on David Hilbert's famous list of 23 unsolved problems that he presented to the mathematical community in 1900. As of today, eight of these problems have been fully proven; three are still unproven; ten are partially proven; and two have been tossed out for being too vague.)

Long story short, Gödel's theorem is both enormously important but also of little use in real life. This is the way of things.

5. Further Reading

If you really want to understand what Gödel did, the indispensable book is Gödel's Proof, by Ernest Nagel and James Newman. It was published the year I was born and is still in print. It does require a modest love of math, but it's only a hundred pages long and is written unusually clearly. Another possible text is Douglas Hofstadter's Gödel, Escher, Bach, which is massively long but also very entertaining. It's not everyone's cup of tea, but it does demonstrate how Gödel's theorem works, and it gets there in very tiny, non-mathematical steps.

¹Actually there isn't one formal system of mathematics, there are many. There's one for geometry, one for set theory, one for arithmetic, etc.

²I am, obviously, using "fairly ordinary" in a very specific sense.

Tyler Cowen directs us to Roland Fryer, writing today about the pay gap for Black workers:

For decades, social scientists have shown that raw gaps in employment outcomes [...] misstate the amount of actual bias in an organization.

....One of the most important developments in the study of racial inequality has been the quantification of the importance of pre-market skills in explaining differences in labor market outcomes between Black and white workers. In 2010, using nationally representative data on thousands of individuals in their 40s, I estimated that Black men earn 39.4% less than white men and Black women earn 13.1% less than white women. Yet, accounting for one variable—educational achievement in their teenage years—reduced that difference to 10.9% (a 72% reduction) for men and revealed that Black women earn 12.7 percent more than white women, on average.

This sounds exactly right. I've taken a look at this several times and found that Black students typically graduate from high school with test scores that place them (on average) at about a 9th or 10th grade reading level compared to 12th grade for white students. When you then compare various life outcomes, including income, of Black workers vs. white workers with 9th grade reading scores, they're nearly equal.

Not completely equal, as Fryer says. There's still a gap left, and the evidence suggests it's probably due to racial discrimination.

I've never been able to reliably get information disaggregated by gender, but what little evidence I've seen suggests that racial discrimination hits Black men harder than Black women. Fryer confirms this in a big way, and the difference remains about the same even after you account for high school education.

Education, as always, is key. If we really want to be anti-racist, improving the education of Black children is something we have to be dedicated to. It's hard, it's expensive, and white people largely hate it. What's more, we've tried and tried for years with little success. But we still have to do it.

This is the Louvre as viewed from the left bank of the Seine. I like this view because it forces me to see the Louvre not as a museum, but as a royal palace, which it was intermittently for three centuries before Louis XIV finally abandoned it for good when he moved to Versailles.

Ironically, although Versailles has a reputation for hugeness, the Louvre is more than three times bigger. The grounds of Versailles, at 2,000 acres, are the largest of any royal residence in the world, but it has only about 700,000 square feet of floor space, which doesn't even rank it in the top ten in Europe. (It's #11.)

In the Washington Monthly, Paul Glastris writes about regulation and monopolies:

Federal regulation is not a hindrance to freedom or prosperity but bulwarks of both. Unfortunately, [in the early '80s], leaders of both parties adopted a contrary set of ideas, dubbed “neoliberalism”: that deregulating markets was the key to economic growth.

Wait. The Monthly is opposed to neoliberalism? They practically invented neoliberalism—though perhaps of a different variety than the one Paul is criticizing. Neoliberalism has so many definitions these days that it's all but impossible to know what people mean when they use the word.

That said, I've never been quite able to join in the progressive revulsion toward neoliberalism. Sure, it went overboard in some places, especially banking, but then there's this:

During the period from 1950-1985 world GDP increased $4,000 on a per capita basis adjusted for inflation. In the following 35 years world GDP increased nearly $8,000.

That's about the same on a percentage basis. But it's twice as much on a dollar basis and it shows more signs of exponential growth than the earlier period—even though the immediate postwar era was famously one of high growth. But starting from a much higher base and without a lot of catchup growth built in, world GDP still grew more strongly under a neoliberal regime. I wonder if it could have done that otherwise.

There are nuances to consider. A big part of recent economic growth has been due to just China and India, which are hardly neoliberal poster children. And the housing bubble and subsequent banking crash of 2008 can plausibly be laid at the feet of deregulation.

For these reasons I'm not an unrestrained booster of neoliberalism. But I still suspect it did more good than harm.

Also, while I'm not a big fan of monopolies, I don't think they have anything to do with our current bout of inflation, which is both temporary and caused by unique factors. For example, an unprecedented global pandemic. But who knows? I'll read Phil Longman's cover story and maybe he'll convince me. He's done it before.

Supreme Court liberals have been caught in public recently praising their conservative brethren. This has provoked the ire of many progressives, who are convinced they must be idiots, but I'd like to propose a radical alternative: the justices might be lying in order to form good relationships with conservatives.

Why? Because when you're in a 6-3 minority you can't do anything unless you manage to persuade a couple of conservatives to vote with you. And it's a lot easier to do that if you make nice internally and praise them externally.

Just a thought.

How is our mental health doing? It's gotten a lot of attention in these post (?) COVID days, some of it based on this Gallup poll from a few months ago:

The line to look at is the "excellent/good" line at the top, and it unquestionably dipped during the height of the pandemic. At the same time, it's now only four points below its pre-pandemic level, which isn't a huge amount. I'd say we came through pretty well.

But the crosstabs are interesting:

Women and 18-34 olds started out low and declined as much as everyone else. Put those two categories together and they spell "mothers," who have probably taken the biggest hit from the pandemic.

Religion sure helped during the pandemic. Before COVID, churchgoers and abstainers both felt the same. But during the pandemic churchgoers remained stable while abstainers plummeted.

It's also remarkable how much better Republicans feel compared to Democrats. Before COVID they registered a remarkable 26 points higher than Democrats. That went down during the pandemic, but even now they clock in 14 points higher. Why? Is it related to moral certitude? The excitement of a big battle? A happiness born of not feeling responsible for people outside your family? Higher average incomes? Anybody have any other ideas?

Tonight I find common bond with the conservative movement in the US on a development that's a threat to all of us. I speak, of course, about QR-code menus in restaurants:

QR-code menus are annoying, but not exactly the greatest civilizational threat of our time. But there’s a serious aspect of this, too: They not only represent a holdover from a pandemic era that we should be leaving in the rearview as expeditiously as possible — they also are another concession to the digitization of American life, replacing the world of the physical and material with an emaciated, online substitute. For that reason, and so many others, we should demand a return to the real thing. Nothing less than physical plastic menus will do.

I'll add this: not only do online menus suck because they're hard to read on a cell phone, but like most technological "improvements" they only work when they're in the right mood. I calculate, based on extensive research, that they operate properly only 64.3% of the time.¹ That's not nearly good enough.

Note that I am fully supportive of online menus in general. They're a great tool for checking out a restaurant beforehand to see if they offer the kind of food your group will like. I just don't want them at the restaurant.

POSTSCRIPT: Yes, I know that restaurants will give you a paper menu if you ask for one. But for how long?

ANOTHER POSTSCRIPT: Before I get a round of "OK Boomer" from the young 'uns, a word of warning: eventually your eyes will deteriorate too and cell phones won't be the delightful experience they are now. Even with bifocals.

On second thought, by the time you're 60 medical science will probably be able to provide you with bionic eyes. Damn.

¹This is a joke. But it does roughly represent my personal experience based on maybe a dozen usages.