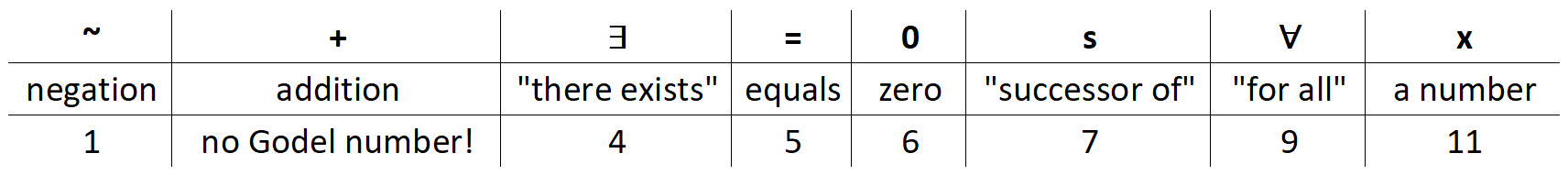Bob Somerby wants to know if the logician/mathematician Kurt Gödel is a genius or a charlatan. The answer is "genius," but it's hard for non-mathematicians to understand his seminal theorem or why it matters. Bob is relying on Rebecca Goldstein's biography of Gödel, and this is a mistake since it's a biography, not a mathematical treatise.
But it's dex night, so I'll take a crack at it. Fair warning: you really need to have at least a little bit of background in math to understand this. There's just no way around it. However, you don't need much as long as you're willing to tolerate a bit of mathematical symbology. Here goes.
1. Mathematical symbols
Although most of us don't think of it this way, mathematics is actually a formal logical system of symbol manipulation.¹ For this to work, it must be possible to express all mathematical statements in a formal symbolic language. And it is! Take this statement, for example:
For every number there is a number that's one higher
In mathematical symbology it looks like this:
∀ x ∃ x + 1
(For all numbers x there exists x + 1)
There is a symbol for anything you can say in the language of mathematics. If you're interested, a complete list is here—though there are some complicated nuances for certain kinds of expressions. Basically, though, there's a symbol for everything, although non-mathematicians are unfamiliar with most of them.
2. Gödel numbering
Gödel's initial insight was that you could assign a unique number to every symbol. Here's a sample:
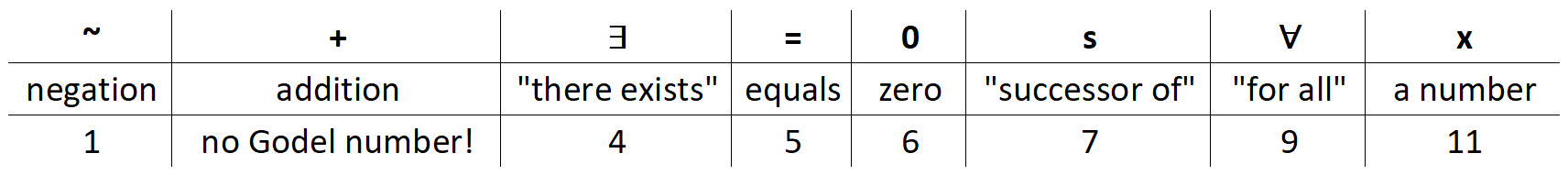 After a bit of rewriting to mathematical standards, our statement from above looks like this:
After a bit of rewriting to mathematical standards, our statement from above looks like this:
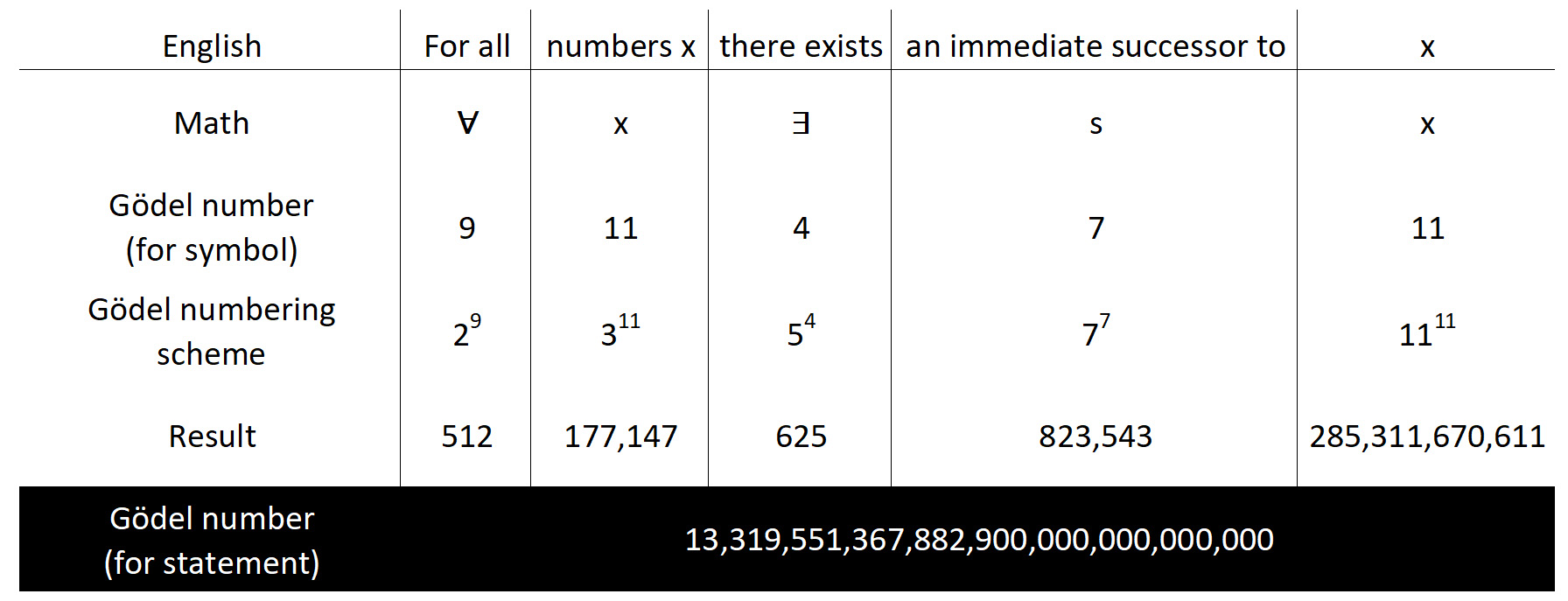 In essence, Gödel numbering is simple. In line 3 we replace every symbol with its Gödel number. In line 4, we take a series of prime numbers starting with two, and raise each one to its Gödel number. The first prime is 2, so we calculate 29. The next prime is 3, so we calculate 311. Etc.
In essence, Gödel numbering is simple. In line 3 we replace every symbol with its Gödel number. In line 4, we take a series of prime numbers starting with two, and raise each one to its Gödel number. The first prime is 2, so we calculate 29. The next prime is 3, so we calculate 311. Etc.
In the final line we multiply all these numbers together to get the Gödel number for the entire statement. It's a big number, and for more complicated statements the number becomes astronomical. But who cares? We don't actually have to calculate this number, we just have to know that it exists and that it's unique. Which it is. That final number represents our statement, only our statement, and there's no other number that also represents our statement. This number is our statement.
3. Gödel's proof
So far, what Gödel has done is inventive and easy to understand. What comes next is world historically insightful and more or less impossible to understand for non-mathematical laymen. But let's go ahead with a simplified version.
Every mathematical system—arithmetic, geometry, set theory, etc.—consists of (1) a set of symbols, (2) a set of rules for constructing statements that are valid expressions (i.e., strings of symbols) but which may be either true or false, (3) a set of rules for manipulating symbols, and finally, (4) a set of axioms to start with. This is called an "axiomatic system," and it's the foundation of nearly all modern mathematics.
A formal proof of a theorem starts with axioms (in symbolic form) and then moves in small steps using valid statements that are created using the rules of manipulation. When this series of statements finally reaches the theorem itself, the theorem is said to be proven.
Any respectable system of mathematics must fulfill two requirements: it must be complete and it must be internally consistent. "Complete" means that every true theorem can be proven. "Consistent" means that it's not possible to prove both a theorem and its opposite. But how do you prove that a mathematical system is both complete and consistent?
It's not easy! David Hilbert, the namesake of one of my cats, famously created an axiomatic system of geometry in 1899, and in 1910 the philosopher/logician Bertrand Russell and his coauthor Alfred North Whitehead produced a massive three-volume work called Principia Mathematica, which attempted to completely systematize arithmetic and set theory and make them both complete and free of contradictions. Along the way, Russell and Whitehead created a remarkably comprehensive system of notation that allowed all statements of arithmetic to be written in a standard manner. It is one of the most famous treatises on logic and mathematics ever written.
But was it correct? In the same way that individual symbols and statements can be reduced to Gödel numbers, an entire proof can also be given a unique Gödel number. Gödel's genius was in realizing that certain properties of these numbers could tell us things. In particular, they could be used to decide whether a system of mathematics was complete and consistent.
And it turns out that no interesting system of mathematics is both. In 1931 Gödel published a famous paper which showed, using Gödel numbers, that assertions about mathematics (for example, "the series of statements with Gödel number x is a proof of the formula with Gödel number y") could be reduced to ordinary statements within mathematics ("x is related to y"—though in a complicated way that we will skip over lightly). This in turn allowed Gödel to demonstrate that in any system of mathematics complex enough to be useful—such as ordinary arithmetic—you can construct at least one statement about arithmetic that (1) can be transformed into a normal statement within arithmetic, (2) can be proven, but (3) only if its opposite can also be proven. That's impossible in any consistent system, which means the statement is unprovable in an allegedly consistent system like arithmetic. But Gödel did more: he showed that even though this statement couldn't be proven, it was clearly true. This means that arithmetic is incomplete: it contains true statements that can't be proven.
Finally, in his coup de grâce, Gödel showed that the statement "arithmetic is consistent" is unprovable within the system of arithmetic itself. In all this he used the notation created in Principia Mathematica, which had been explicitly designed to create a system of arithmetic and formal logic that was complete and internally consistent. The result was a proof that Russell and Whitehead were wrong. No system of mathematics is both complete and consistent.
That was a kick in the gut.
4. But what does it all mean?
In day-to-day use, Gödel's theorem plays no role. In fact, a few years after it was published a fellow German mathematician proved that for all practical purposes the system of arithmetic we use (based on the Peano postulates, a set of five axioms for the natural numbers created by Giuseppe Peano in 1889) is indeed consistent. Workaday math is in fine shape, and most working mathematicians go through life never knowing anything about Gödel, who is of interest mostly to abstract logicians.
But on an abstract level Gödel's theorem was both a bombshell and a source of dismay. What's more, it does come into play sometimes in fairly ordinary mathematics.² For example, transfinite math defines various types of infinity, and the two smallest types of infinity correspond to the set of integers (represented as ℵ0, or "aleph nought," because mathematicians like to fuck with us) and to the set of real numbers (represented as C, because mathematicians like to fuck with us). But is there any infinity between those two? In 1966 Paul Cohen won a Field Medal for using Gödel's theorem to show that this was impossible to prove one way or another.
(This is called the Continuum Hypothesis, first proposed by Georg Cantor, the inventor of transfinite mathematics. He believed there was no infinity between ℵ0 and C, and this was #1 on David Hilbert's famous list of 23 unsolved problems that he presented to the mathematical community in 1900. As of today, eight of these problems have been fully proven; three are still unproven; ten are partially proven; and two have been tossed out for being too vague.)
Long story short, Gödel's theorem is both enormously important but also of little use in real life. This is the way of things.
5. Further Reading
If you really want to understand what Gödel did, the indispensable book is Gödel's Proof, by Ernest Nagel and James Newman. It was published the year I was born and is still in print. It does require a modest love of math, but it's only a hundred pages long and is written unusually clearly. Another possible text is Douglas Hofstadter's Gödel, Escher, Bach, which is massively long but also very entertaining. It's not everyone's cup of tea, but it does demonstrate how Gödel's theorem works, and it gets there in very tiny, non-mathematical steps.
¹Actually there isn't one formal system of mathematics, there are many. There's one for geometry, one for set theory, one for arithmetic, etc.
²I am, obviously, using "fairly ordinary" in a very specific sense.
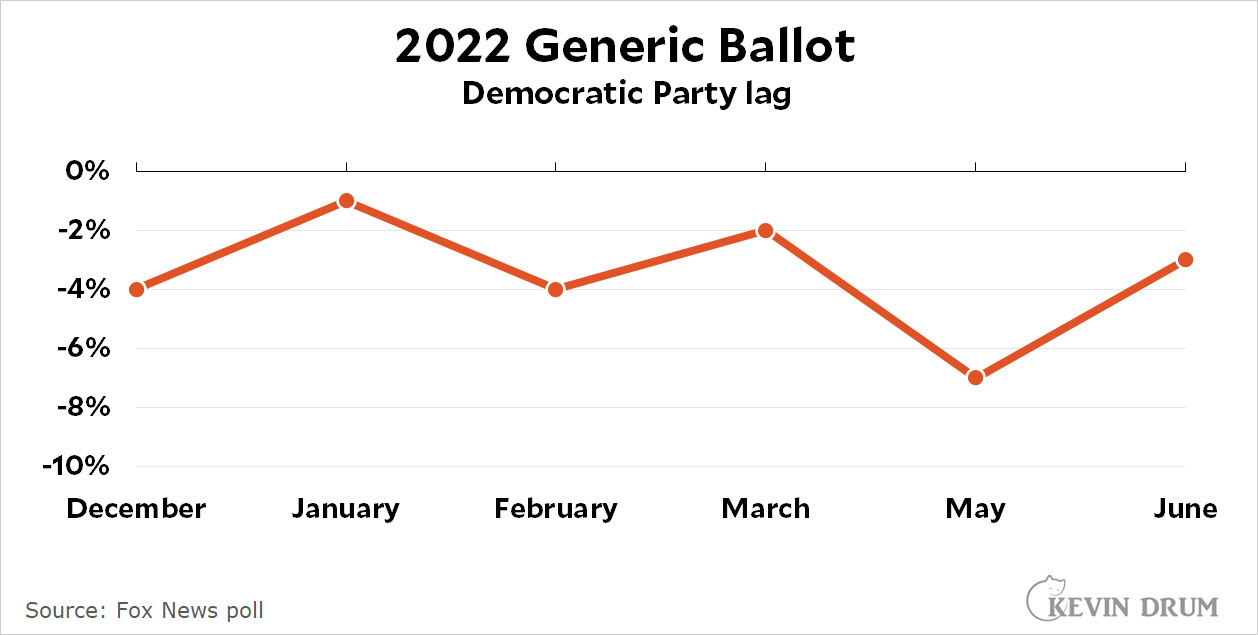
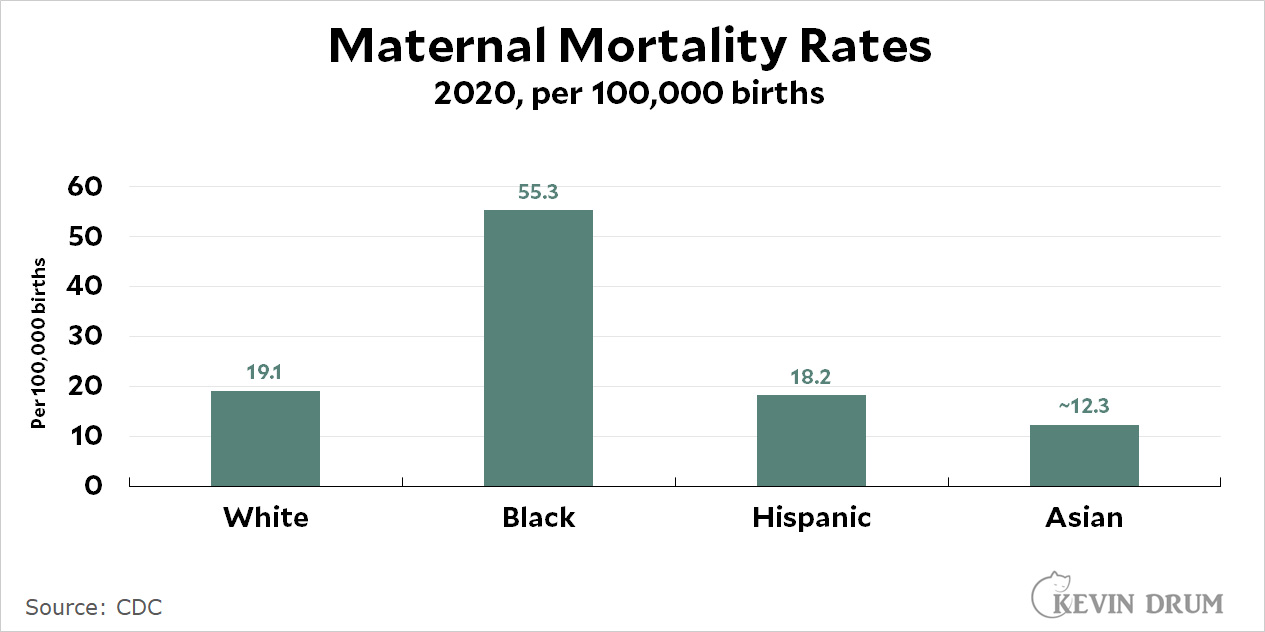
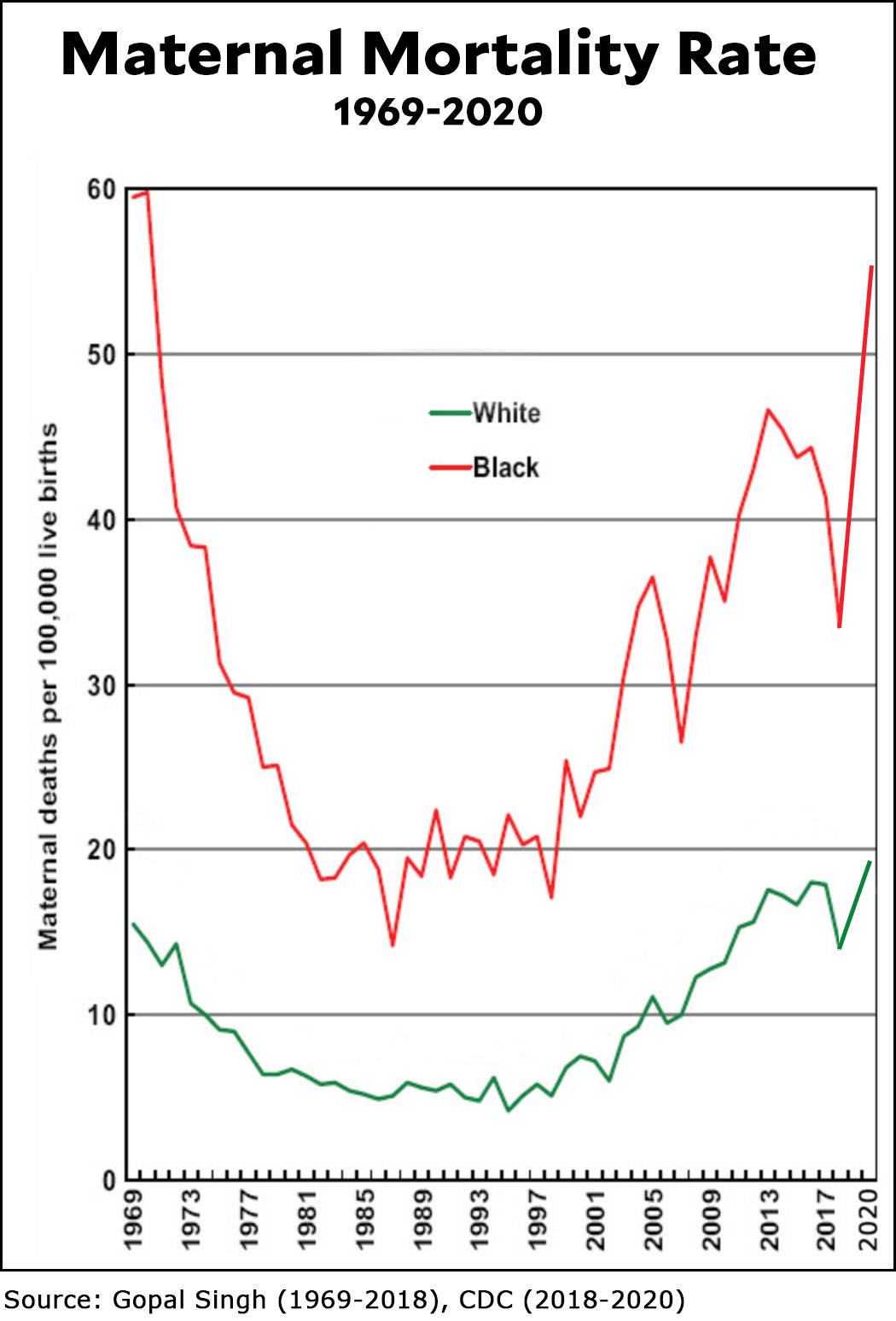
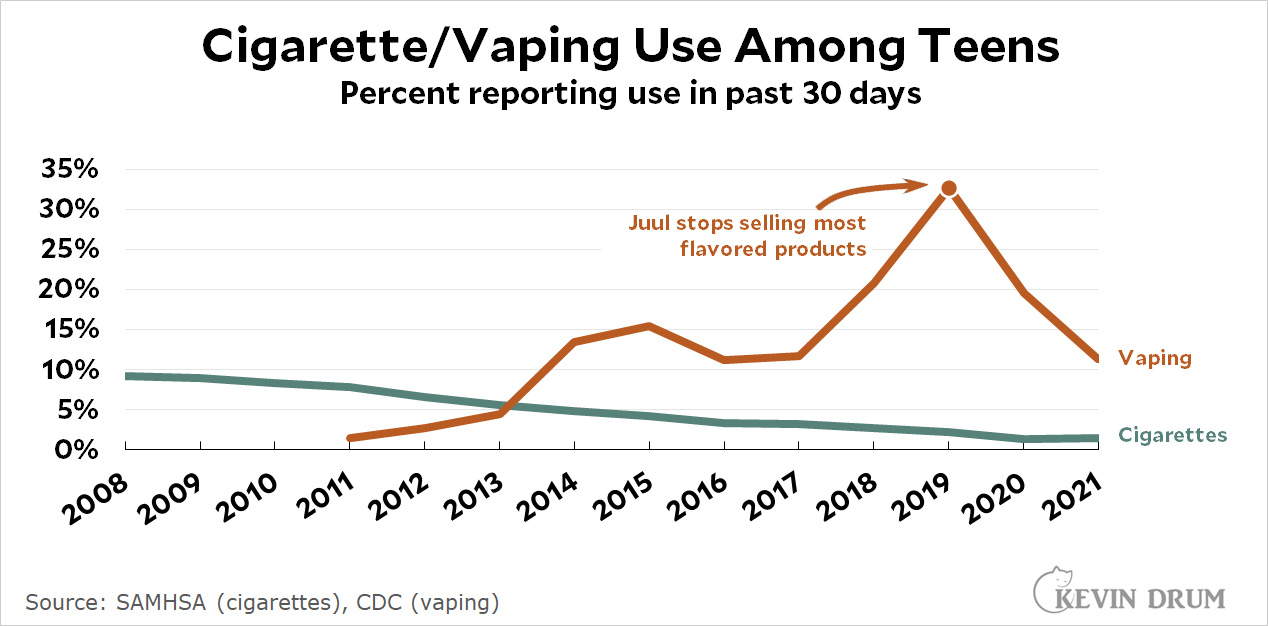 Most teen vaping (roughly 80%) is nicotine vaping, and it's obviously bad to get kids hooked on nicotine. On the other hand, vaping is better than cigarette smoking, so if more vaping leads to lower cigarette use then it might be a net positive.
Most teen vaping (roughly 80%) is nicotine vaping, and it's obviously bad to get kids hooked on nicotine. On the other hand, vaping is better than cigarette smoking, so if more vaping leads to lower cigarette use then it might be a net positive.